Contributing to better decision-making in public policy to face the health challenges posed by the current Covid-19 pandemic situation is one of the objectives of the study developed by Yissedt Lara. Temporal an Spatial Modeling of Infectious Diseases, Invasive Forest Insects and Biological Control is the name of the research thesis that Yissedt develops as part of her studies in the PhD program in Applied Sciences with a minor in Mathematical Engineering from the Universidad de Concepción, UdeC, under the direction of Raimund Bürger (Center for Research in Mathematical Engineering, CI²MA) and Gerardo Chowell-Puente (School of Public Health Georgia State University, USA). Both academicians have collaborated for years on related topics, and in 2018, Chowell visited UdeC using funding from project CONICYT/MEC80170119  in which he taught a course on mathematical epidemiology, an opportunity that Yissedt took chance of to strengthen collaborative contacts with both, given her interest in developing her thesis on these subjects. This initial collaboration resulted in their first joint publication in a specialized magazine.

About the contents of her research with applications in the context of the current health emergency, Yissedt details that “the main objective of my research is the study of epidemiological models and biological control. Some of these models are characterized in that we can define where new infections will occur or not, that is, it defines the number of secondary cases generated from the first infected individual, which sets an alert to apply restrictive measures or policies among the populations involved, because what is sought is to control, eradicate or decrease the infection rate”, she details. The graduate student explains that “these measures or policies can be expressed in new mathematical models, and thus observe whether there will be new cases or not. These models can be simple or very complex since they can even incorporate mobility between people” and she explains that, “for all these applications, we are leaning on ordinary and partial differential equation theory, numerical analysis and methods, some statistical concepts and the data management to create realistic computational simulations”.

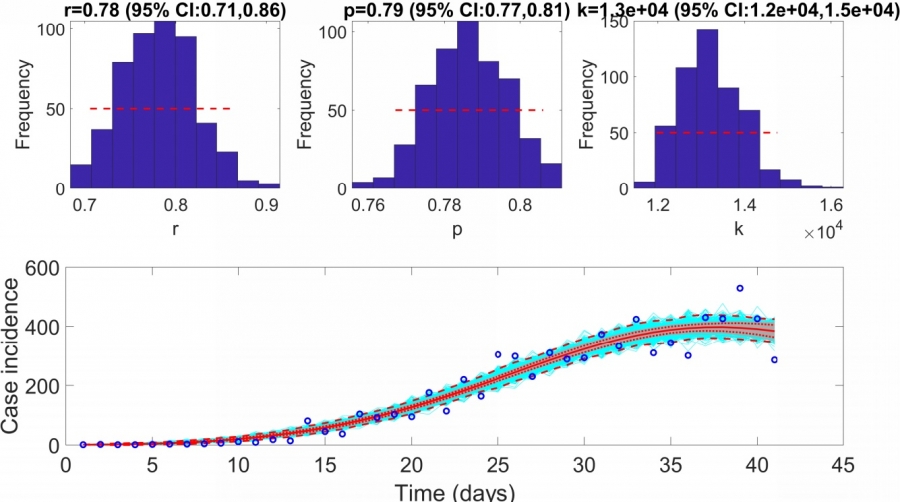
Yissedt explains that with the results obtained so far, “we have verified that, among different phenomenological growth models, the fit of the generalized logistic growth model stands out, both in real and simulated data. This type of study is important because it allows us to distinguish and characterize the best growth models to adjust the data collected in a real situation of outbreak and contagion, and thereby develop good short-term forecasts, certainly relevant when taking action of mitigation or control”. Regarding future challenges in her research, the student explains that, in the short term, “what follows is to raise, adjust and simulate more situations that are present in the development of an outbreak. For example, currently due to the SARS-CoV-2 coronavirus, we have changed our daily routine by being under measures of social distancing or quarantines, and with such situations we are currently working to model and forecast the evolution of Covid-19 in Chile. We plan to incorporate into a mathematical model by compartments, the recent measures of school activities suspension, social distancing, quarantines and sanitary cords, as well as the massive use of masks and gloves, where we will see how such measures affect or how much the number of new cases decreases”.

Based on the results already achieved in her thesis, Yissedt states that, as the figure below shows, “the evolution of Covid-19 cases in Chile shows sub-exponential growth. This may be due to the measures taken by the government, but that is something that we want to study further in our next research, with the application of control measures to the model”, says the student whose research is funded by the Doctoral Scholarships Program of the National Agency for National Research and Development ANID/21190640.